Voorbeelden van Mathekalender-opgaven
Hieronder staan twee voorbeelden van Mathekalender-opgaven: eentje in het Nederlands, eentje in het Engels (sinds een aantal jaar de voertaal van de kalender). Nog veel meer opgaven -en uitwerkingen- vind je in het Opgavenarchief.
Opgave 1: Spelen met koffers
In een lange rij staan 101 koffers, die op een lopend genummerd zijn met de getallen 0,1, 2, ..., 100. De Grinch en Knecht Ruprecht spelen met deze koffers het zogenaamde T-koffer-spel (waarbij T een positief geheel getal is).
 De Grinch kiest twee getallen x en y met 0≤x≤100, 0≤y≤100 en |x-y|≤50, en verstopt een kurkentrekker in koffer x en een fles rum in koffer y. Alle andere koffers blijven leeg. Knecht Ruprecht mag dan in de rij in totaal T koffers openmaken: de eerste koffer mag Ruprecht willekeurig kiezen. Elke volgende koffer mag alleen geopend worden, wanneer aangrenzend links of rechts daarvan reeds een koffer geopend is. Knecht Ruprecht wint het spel, wanneer hij zowel de kurkentrekker als de fles rum vindt; anders wint de Grinch. Beide spelers maken hun keuzes die voor henzelf het meest gunstig zijn.
De Grinch kiest twee getallen x en y met 0≤x≤100, 0≤y≤100 en |x-y|≤50, en verstopt een kurkentrekker in koffer x en een fles rum in koffer y. Alle andere koffers blijven leeg. Knecht Ruprecht mag dan in de rij in totaal T koffers openmaken: de eerste koffer mag Ruprecht willekeurig kiezen. Elke volgende koffer mag alleen geopend worden, wanneer aangrenzend links of rechts daarvan reeds een koffer geopend is. Knecht Ruprecht wint het spel, wanneer hij zowel de kurkentrekker als de fles rum vindt; anders wint de Grinch. Beide spelers maken hun keuzes die voor henzelf het meest gunstig zijn.
We definiëren p (respectievelijk q en r) als de kans dat Ruprecht het 60-kofferspel (respectievelijk het 70-kofferspel, en het 80-kofferspel) wint. Welke van de volgende uitspraken is waar?
1. p = 30/101, en q = 40/101, en r = 50/101.
2. p = 60/101, en q = 70/101, en r = 80/101.
3. p = 3/9, en q = 4/9, en r = 5/9.
4. p = 3/10, en q = 4/10, en r = 5/10.
5. p = 3/11, en q = 4/11, en r = 5/11.
6. p = 3/12, en q = 4/12, en r = 5/12
7. p = 1/6, en q = 1/3, en r = 2/3.
8. p = 1/4, en q = 1/3, en r = 1/2.
9. p = 1/3, en q = 1/3, en r = 1/3.
10. p = 1/3, en q = 1/3, en r = 1/2.
Oplossing opgave 1
Wij maken een analyse die alle mogelijke waarden van T in beschouwing neemt.
Het is duidelijk dat voor T<50 Grinch altijd wint door bijvoorbeeld de kurkentrekker in koffer 0 en de fles rum in koffer 50 te verbergen. Voor T = 101 is natuurlijk altijd knecht Ruprecht de winnaar; hij mag immers alle 101 koffers openen. Wij tonen nu aan dat de kans dat Ruprecht wint gelijk is aan 1/3 indien 51≤T≤75 en gelijk is aan 1/2 indien 76≤T≤100. Daarmee is optie 10 het correcte antwoord.
(1) Voor 76≤T≤100 wint Ruprecht het spel met een kans hoogstens gelijk aan 1/2: Met kans 1/2 verstopt Grinch beide voorwerpen in koffer 0 en met kans 1/2 verstopt hij de beide voorwerpen in koffer 100. Omdat Ruprecht hoogstens één van de beide koffers 0 en 100 kan openen zal zijn kans om te winnen nooit groter zijn dan 1/2.
(2) Voor 51≤T≤75 wint Ruprecht het spel met kans hoogstens gelijk aan 1/3: Met kans 1/3 verstopt Grinch beide voorwerpen in de koffers 0 en 25 (Mogelijkheid A), met kans 1/3 in de koffers 25 en 75 (Mogelijkheid B) en met kans 1/3 in de koffers 75 en 100 (Mogelijkheid C). Omdat Ruprecht hooguit één van de koffers 0 en 75 mag openen en hoogstens één van de koffers 25 en 100, hoeft hij hoogstens één van de drie mogelijkheden A, B, C verder te inspecteren.
(3) Voor76≤T≤100, wint Ruprecht het spel met een kans minstens gelijk aan 1/2: Met kans 1/2 opent Ruprecht de koffers 25, ..., 75 (Mogelijkheid A) en met kans 1/2 opent hij de koffers 25, ..., 100 (Mogelijkheid B). In geval Grinch beide voorwerpen in de koffers 0, ..., 75 verstopt, dan wint Ruprecht met kans 1/2 bij mogelijkheid A. In geval Grinch een of beide voorwerpen in de koffers 76, ..., 100 verstopt, dan wint Ruprecht met kans 1/2 bij mogelijkheid B.
(4) Voor 51≤T≤75 wint Ruprecht het spel met een kans van tenminste 1/3:
- Mogelijkheid A: Met kans 1/3 opent Ruprecht de koffers 0, 1,..., 50.
- Mogelijkheid B: Met kans 1/3 opent Ruprecht de koffers 50,..., 100.
- Mogelijkheid C: Met kans 1/3 opent Ruprecht in eerste instantie de koffers 50, 51, 52, ... Indien hij een voorwerp ontdekt, dan opent hij daarna de koffers 49, 48, 47, ....
Indien Grinch beide voorwerpen in de koffers 0, ..., 50 verstopt, dan wint Ruprecht met een kans van 1/3 bij mogelijkheid A.
Indien Grinch beide voorwerpen in de koffers 50, ..., 100 verstopt, dan wint Ruprecht met een kans van 1/3 bij mogelijkheid B.
Indien Grinch een van de twee voorwerpen in de koffers 0, ..., 49 verstopt, en de andere in de koffers 51,... 100, dan wint Ruprecht bij mogelijkheid C met een kans van 1/3.
Opgave 2: Rowdy Reindeer
Santa has a stable for his reindeer, which is divided into nine enclosures as shown in Figure 1.
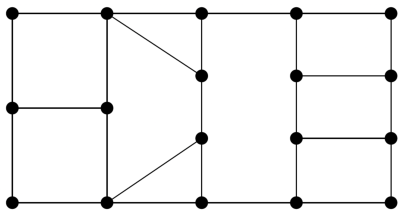
Figure 1: Santa’s stable.
 Santa’s elves have ordered red-nosed and brown-nosed reindeer to fill these nine enclosures. Unfortunately, something went wrong: instead of nine reindeer they accidentally ordered twelve. To make it even worse, the reindeer are very territorial: the enclosures of any two brown-nosed reindeer cannot share a wall without the reindeer fighting, and the same holds for the enclosures of any two red-nosed reindeer. Fortunately, a reindeer will never fight with a reindeer whose nose has a different color; so the enclosures of a red-nosed reindeer and a brown-nosed reindeer can share a wall. Also, there will never be any fighting between reindeer whose enclosures only meet in a corner, or do not meet at all.
Santa’s elves have ordered red-nosed and brown-nosed reindeer to fill these nine enclosures. Unfortunately, something went wrong: instead of nine reindeer they accidentally ordered twelve. To make it even worse, the reindeer are very territorial: the enclosures of any two brown-nosed reindeer cannot share a wall without the reindeer fighting, and the same holds for the enclosures of any two red-nosed reindeer. Fortunately, a reindeer will never fight with a reindeer whose nose has a different color; so the enclosures of a red-nosed reindeer and a brown-nosed reindeer can share a wall. Also, there will never be any fighting between reindeer whose enclosures only meet in a corner, or do not meet at all.
The elves cannot change the total number of reindeer they have already ordered, but they can still choose the number of red-nosed and brown-nosed reindeer they receive. To accommodate the twelve reindeer, the elves need to create exactly three new enclosures within the existing stable. For this purpose, they to are instructed to build exactly three new straight walls. Each of the new walls must be put in between two points where already at least two walls meet. These 18 points are marked in Figure 1. Furthermore, the new walls are neither aloud to cross the old walls nor other new ones.
In how many ways can the elves build the three new straight walls, such that it is possible to give each of the twelve reindeer its own enclosure without any reindeer fighting?
Possible answers:
- Zero ways, i. e. it is not possible build the three walls as required.
- One way.
- Four ways.
- Five ways.
- Six ways.
- Eight ways.
- Nine ways.
- Twelve ways.
- Fourteen ways.
- Sixteen ways.
Oplossing opgave 2
Klik hier voor de oplossing.



